Fractals in PyTorch

I have tried implementing fractals in Python before by looping through the pixels, but they were very slow to run compared to my C++ implementations. Then I realized that fractals such as Mandelbrot and the Abelian Sandpile can be much more efficiently computed by vectorizing the pixel computations into matrices/tensors in linear algebra frameworks such as PyTorch and NumPy.

Mandelbrot

The Mandelbrot was the most straight-forward to implement using complex matrices (For Mandelbrot zoom animations doubles and torch.complex128 have to be used). The code is extremely simple, with the core loop consisting just of two lines (Full code here):

#[...]
# define the matrix with the pixel's cooordinates
x = torch.linspace(x_center-diameter, x_center+diameter, resolution, dtype=torch.float64)
y = torch.linspace(y_center-diameter, y_center+diameter, resolution, dtype=torch.float64)
xv, yv = torch.meshgrid(x, y)

# complex matrix defined by coordinates
C = xv + 1j*yv

current = torch.zeros_like(C, dtype=complex_float_type)
output  = torch.zeros_like(C, dtype=torch.int64)

for i in range(1,iterations):
    current = current**2 + C
    output[torch.absolute(current)>2*2] = i
[...]

Buddhabrot

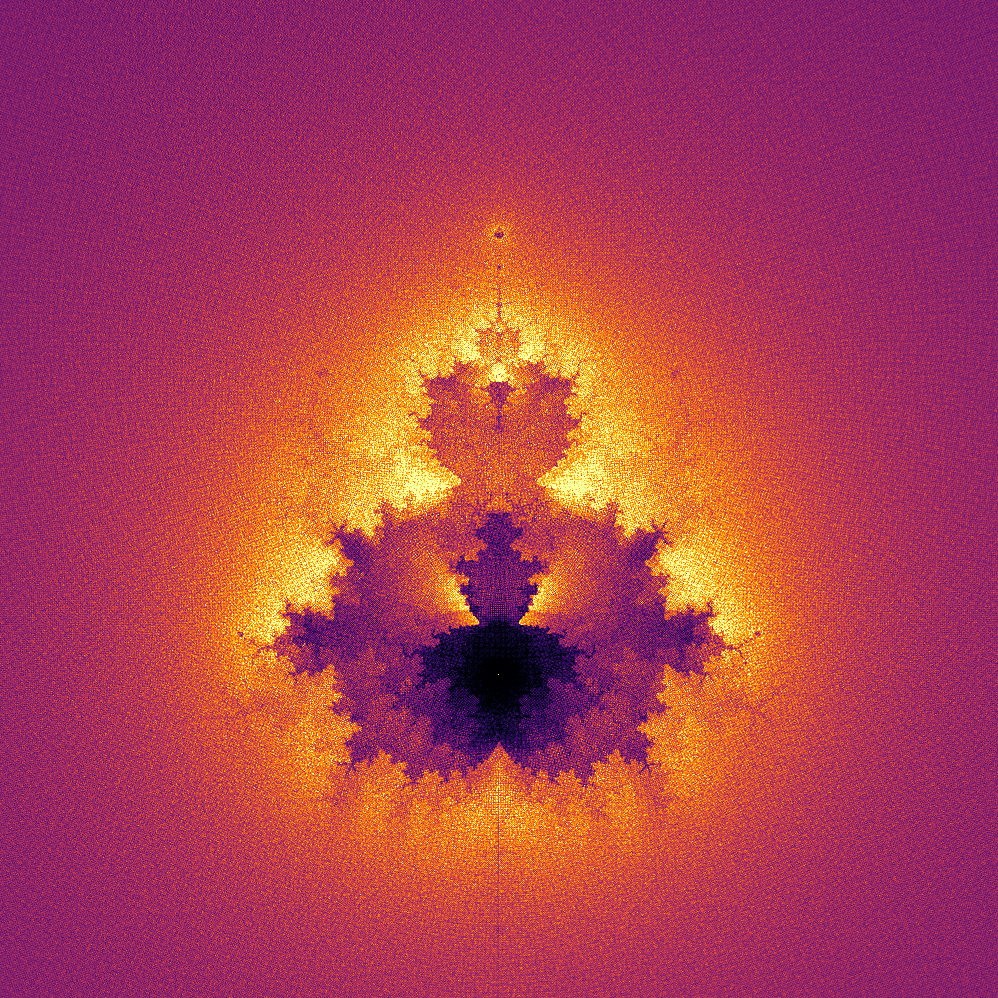
The Buddhabrot was more difficult to implement, since you have to keep track of where the pixels that end up outside the Mandelbrot set were before (Full explanation on Wikipedia). Here we have a memory/time tradeoff: Either we store the past positions of each pixel or we run the loop twice: Once to find out which pixels will end up outside the Mandelbrot set and once to count which coordinates these pixels visited before that. I currently use the first option for speed and the memory impact is acceptible for small numbers of iterations. To count the number of pixels that have visited each position, I used a trick that I learned from segmentation loss functions during my Master’s thesis: Each position (x,y) gets assigned a number j = x + y*resolution and then the occurances of each position is counted using torch.bincount(j.flatten()).

(Full code here)

#[... with C and current defined as above with random pertubations inside the pixel's box]
counts  = torch.zeros(resolution**2)
past_positions = []

for i in range(1,iterations+1): #200):
    current = current**2 + C
    past_positions.append(current)

for i,p in enumerate(past_positions):
    # zero out pixels that don't escape
    p[torch.absolute(current)<2*2] = 0

    # align all pixels so that the pixel with smallest Real and Imag part is the first in the matrix
    p_aligned = p - (x_center-diameter+1j*(y_center-diameter))
    # make everything integers
    p_aligned = p_aligned/(2*pixel_width)
    # round to integer coordinates and restrict to image size
    real = torch.clamp(p_aligned.real.int(),min=0,max=resolution)
    imag = torch.clamp(p_aligned.imag.int(),min=0,max=resolution)
    # assign a number for each coordinate
    coords = real + imag*resolution
    # count occurances of each coordinate
    counts += torch.bincount(coords.flatten(), weights=None, minlength=resolution**2)[:resolution**2]

Abelian Sandpile

I learned about the Abelian Sandpile fractal from this Numberphile video. It looked interesting and I liked the emergence of a Sierpinski triangle pattern. When a pixel reaches a value of four or larger, it topples and the value of the directly neighboring pixels is incremented by one. This behaviour can be efficiently computed by a 2D-convolution with the kernel that is zero everywhere, but marks the position of each neighbor of the center pixel with a one:

(Full code here)

overflow_kernel = torch.tensor([
    [0,1,0],
    [1,0,1],
    [0,1,0]])
overflow_kernel = overflow_kernel.view((1,1,3,3))

grid = torch.zeros((1,1,n,n), dtype=int)
for i in range(iterations):
    grid[:,:,n//2,n//2] += 1
    # numbers four or higher spill over to their neighbors and get reset
    overflow = (grid >= 4).long()
    grid -= 4*overflow
    # add 1 to neighbors of overflowing pixels
    grid += func.conv2d(overflow, overflow_kernel,stride=(1,), padding=(1,)).long()